7931のあたまんなか

数学／読書メモ／自分の考え方／水曜どうでしょう／交通関係（道路・航空）など、頭の中にあることを書き出しています。

『数学の大統一に挑む』の数学部分をまとめてみた

数学 読書メモ

私が学生時代に専門にしていたリー群の表現論が書かれているということを聞き、エドワード・フレンケル『数学の大統一に挑む』を読みました。

数学の大統一に挑む

数学の大統一に挑む

Amazon

この本は、大きく分けて2つのことが書かれています。

1つは、旧ソ連で生まれ育ったフレンケル教授の半生と数学の研究について。
もう1つは、数学と物理（特に量子力学）の関係性をラングランズ・プログラムの説明をしながら描いています。

数学と物理の関係については、かなり専門的な部分まで踏み込んで書かれていて非常に興味を持ちました。

その内容を少しでも理解したいと思い、ノートを取りながら読みました。本文や注釈の内容を自分なりに整理し、手元にある数学書を調べながら書いてまとめました。

数学部分をメモしたノート

数学部分に興味がある方がいるかもしれないので、ノートの内容をこちらで公開します。 *1
ダウンロードはこちらから。

【キーワード】 ラングランズ・プログラム / 群の表現 / フェルマーの最終定理 / ガロア群 / 保型関数 / 調和解析 / リーマン面 / リー群 / 基本群 / ループ群 / 圏 / 層 / ラングランズ双対群 / モノドロミー / ゲージ群 / ゲージ理論 / 場の量子論 / 超対称性 / 有効理論 / シグマモデル / ターゲット多様体 / ヒッチン・モジュライ多様体 / ミラー対称性 / 超ひも理論

フレンケル教授の講義をYouTubeで見ることができます

NHKで放送されたフレンケル教授の講義『数学ミステリー白熱教室～ラングランズ・プログラムへの招待』がYouTubeで見ることができます。

【第1回】
www.youtube.com

【第2～4回】
Mysteries of Math and the Langlands Program - Episode 2 - YouTube
Mysteries of Math and the Langlands Program - Episode 3 - YouTube
Mysteries of Math and the Langlands Program - Episode 4 - YouTube

これから読んでみたい本

『数学の大統一に挑む』を読んでから、数理物理学に興味が出てきました。

関連する本として、これから読んでみたい本がこちらです。私の本棚にはすでに並んでいます。

エレガントな宇宙―超ひも理論がすべてを解明する

エレガントな宇宙―超ひも理論がすべてを解明する

Amazon
超ひも理論をパパに習ってみた 天才物理学者・浪速阪教授の70分講義 (KS科学一般書)

超ひも理論をパパに習ってみた 天才物理学者・浪速阪教授の70分講義 (KS科学一般書)

Amazon

*1:本当はもっとまとめてから公開しようと思っていましたが、予想以上に負荷がかかりそうなので、手書きノートの段階で公開します。

特集「大学数学のキーポイント」～『数学セミナー 2019年4・5月号』読書メモ

数学 数学セミナー 読書メモ

『数学セミナー 2019年4月号』と『数学セミナー 2019年5月号』には、特集「大学数学のキーポイント」が前篇・後篇に分けて書かれています。

数学セミナー 2019年 04 月号 [雑誌]

数学セミナー 2019年 04 月号 [雑誌]

数学セミナー 2019年 05 月号 [雑誌]

数学セミナー 2019年 05 月号 [雑誌]

大学数学の勉強の心構えや仕方、いろいろな数学分野のポイントが書かれています。

特に印象に残った内容について、この記事でまとめます。

数学書の選び方・読み方 *1

  • 教科書スタイルと自由形スタイルの使い分け *2
  • 同じテーマの複数の本を手に取って、自分に合うものを探してみる。
  • 読んでわからなければ、いったん寝かせることもあり。

線形代数や微分積分を学ぶ理由 *3

数学的対象を「よくわかる」ものに近似して考えたい。

代数学をどう理解していくか *4

(1) 群・環・体の例は、小中学校から学んできた数（実数、整数など）で触れている。

  • 例：剰余環（例えば \mathbb{Z} / 2 \mathbb{Z} ）の最も身近な例は「奇数＋偶数＝奇数」「奇数×偶数＝偶数」などの関係。

(2) 代数的対象の具体例を考えると、解析学の命題を代数学の言葉で言い換えることができ、代数学や層の理論で考察を進めることができる。

  • 例：領域上の正則関数全体をなす環を考えると、複素関数論での一致の定理の言い換えができる。

解けない微分方程式との付き合い方 *5

様々な現象をモデル化して微分方程式で定式化することはよく行われるが、具体的に解ける微分方程式はきわめて少ない。そのため、「具体的な解を構成できないからあきらめる」ではなく、微分方程式の解の性質を知ることが目標になる。
そのアプローチはいくつかある。

  • (1) 力学系理論＝“幾何学的に”解く
  • (2) 数値解法＝“計算機で”解く
  • (3) 解が存在する関数空間を考える。

確率変数の見方 *6

高校までで学んだ数を「固い数」と考えると、確率変数で指定される1点はゆらぎを持った「やわらかい数」と考えることができる。

そう考えると、確率統計で扱う内容が見通しよく見えるかもしれない。

複素関数での様々な定義や定理の見方 *7

(1) 実関数の微分可能性と比較すると、複素関数の正則性は非常に強い条件である。

(2) 複素関数では「任意の点で連続だが、任意の点で微分不可能な関数」を得ることは容易（例： f(z) = \overline{z} ）。実関数では難しい（例：ワイエルシュトラスの関数、高木関数）。

(3) コーシー-リーマンの方程式の導出：実軸上の点 h で h \to 0 とした極限と、虚軸上の点 ih で h \to 0 とした極限が一致することを考えればよい。

(4) e^{iz} = \cos z + i \sin z を考えると、実関数では指数関数が単調増加関数だったが、複素関数では周期 2 \pi i の周期関数になる。

(5) ある条件で単純閉曲線上での積分値が 0 になることを主張するコーシーの積分定理は、閉曲線上の1点 a から a までの積分が 0 であると考えると、実関数では当然に成り立つ \int_{a}^{a} f(x) dx = 0 との類似に見える。

(6) リュービルの定理 *8 の見方：実関数では \sin x は有界だが、複素関数 \sin z は非有界である（虚軸上の値 \sin (iy) は非有界 *9 ）。

(7) 一致の定理 *10 の見方：正則関数は正則性を保ったまま一部分の値だけを変えることは不可能である。実関数では容易に得られる。

物理で使う数学 *11

(1) 物理学の習得に向けては「物理現象の記述に必要な数学」をあらかじめ学ぶ。 *12

(2) 物理を理解するためには、分野によっては偏微分方程式／微分形式／微分幾何学／リー代数など多岐にわたる。すべてを詳しく知らなければならないというわけではない。

*1:『数学セミナー 2019年5月号』の「数学書の選び方・読み方」より

*2:個人的には、自由形スタイルの数学書を多く読みたいという思いがある。

*3:『数学セミナー 2019年4月号』の「線形代数」と「微分積分で学ぶこと」より

*4:『数学セミナー 2019年5月号』の「群と環 ― 透き通った言葉として」より

*5:『数学セミナー 2019年5月号』の「「微分方程式論」の道しるべ」より

*6:『数学セミナー 2019年5月号』の「時代が求める確率統計」より

*7:『数学セミナー 2019年5月号』の「複素関数論入門」より

*8:[tex: \mathbb{C} 全体で有界な正則関数は定数関数である。

*9: y \ge 0 では | \sin (iy) | \ge e^y / 2 で、 y \to \infty とするとわかる。

*10:定義域内に集積点を持つような可算点列上で値が一致すれば、定義域全体で関数が一致する。

*11:『数学セミナー 2019年5月号』の「物理数学」より

*12:私は数学科出身なので、実態はよくわかりません。

d次元ルベーグ測度～『ルベーグ積分講義』読書メモ

数学 読書メモ

『ルベーグ積分講義』（新井仁之 著）の読書メモ第4回です。

ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち

ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち

第Ⅰ部「面積とは何か」の最後のまとめです。

これまでの読書メモはこちらです。

今回は第6章「d次元ルベーグ測度」のまとめです。

一般の次元のルベーグ測度

第5章までで議論されてきた2次元実数空間 \mathbb{R}^2 のルベーグ測度を拡張して、第6章では一般の d 次元実数空間 \mathbb{R}^d のルベーグ測度を定義します (d = 1,2,\dots) 。

2次元で成立する各命題は、 d 次元でも同様に成立することが説明されています。

第6章の主張と第1～5章の主張の対応

第6章で説明されているいろいろな定義や定理は、第1～5章の定義や定理に対応しており、証明も同様にできます。

ここではその対応をまとめます。

第6章の主張 対応する第1～5章の主張 備考
定義6.1 定義1.2 基本直方体、基本立方体
定義6.2 定義2.1 ルベーグ外測度
定理6.3 定理2.16
定理6.4 定理3.2 ルベーグ外測度の劣加法性
定義6.5 例2.2 （有界）閉集合
定義6.6 定義2.7 ルベーグ内測度
定義6.7 定義2.10, 定義3.18 ルベーグ可測集合、ルベーグ測度
定義6.8 定義3.10 開集合
定理6.9 定理3.16'
開集合はルベーグ可測 系3.15'
閉集合はルベーグ可測 系3.9'
定理6.10 (1) 定理4.1
定理6.10 (2) 定理3.1' ルベーグ測度の完全加法性
定理6.11 (2)の条件 定義5.1 カラテオドリの可測性
定理6.11 定理5.5 ルベーグ可測とカラテオドリ可測が同値
系6.12 系4.3 等測核、等測核
定義6.13 命題2.11 (2) 零集合
系6.14 系4.4
定理6.15 定理4.5

カラテオドリの意味での可測性～『ルベーグ積分講義』読書メモ

数学 読書メモ

『ルベーグ積分講義』（新井仁之 著）の読書メモ第3回です。

ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち

ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち

Amazon

これまでの読書メモでは、 ジョルダンとルベーグの2つの方式での面積の定義 と ルベーグ測度の性質 について整理しました。

今回は第5章のまとめです。

カラテオドリによるルベーグ可測性の特徴づけ

上にあるこの節の見出しは、第5章のタイトルそのものにしました。

第2章で定義されたルベーグ可測性と同値なものとして、カラテオドリによる可測性の定義があることが、この章を通じて説明・証明されています。

ルベーグ測度は「ルベーグ外測度＝ルベーグ内測度」で定義されました。

カラテオドリの意味で可測であることは、ルベーグ外測度のみで記述されます。（定義5.1）

これまでに説明されているジョルダン可測性やリーマン可積分性との関係をまとめると、次のような図で表現できます。


補足

命題5.1について

  • 主張：定理4.1との類似性に注目する。
    • 定理4.1の \mathfrak{M} を \mathfrak{M}^* に置き換えたものが命題5.1の主張である。
  • 証明：定理4.1の位相空間論を使った証明とは異なる。

定理5.5の証明

  • 81ページ6行目：定理3.1'を使う。
  • 81ページ8～9行目：開集合 G と集合 G \cup A, \ G \cap A^c はルベーグ可測であること（系3.15と定理4.1より）と定理3.1'より、8行目の最右辺を得る。また、ルベーグ可測集合 B に対して m(B) = m^* (B) であることと E \cap A \subset G \cap A 、および補題2.9より、9行目を得る。
  • (2)⇒(1)の証明で開集合 G と U をとれる理由：補題3.17の(i)と(ii)を繰り返し適用すればよい。
  • (2)⇒(1)の m^*(A) = \infty の場合の証明の結末： A_n がルベーグ可測であることと A= \bigcup_{n=1}^{\infty} A_n および定理4.1 (4)から、 A がルベーグ可測になる。

ルベーグ測度の性質〜『ルベーグ積分講義』読書メモ

数学 読書メモ

『ルベーグ積分講義』（新井仁之 著）の読書メモ第2回です。

ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち

ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち

Amazon

前回の読書メモでは、ジョルダンとルベーグの2つの方式での面積の定義について整理しました。

wed7931.hatenablog.com

今回は、第3〜4章に書かれているルベーグ測度の性質をまとめます。

第3〜4章を読む上で注意すること

  • 各主張がルベーグ測度 or ルベーグ外測度のどちらに関することか？
  • ルベーグ測度が有限 or 一般の場合（有限とは限らない）か？
    • 全般的に、前半で有限の場合、後半で一般の場合を示している。

2つの加法性

  • ルベーグ測度は完全加法性（または σ-加法性）を持つ。
    • 有限の場合：定理3.1、一般の場合：定理3.1’
  • ルベーグ外測度は劣加法性を持つ。
    • 一般の場合：定理3.2（有限の場合を含む）
  • ルベーグ外測度が完全加法性を満たすかは難しい問題
    • 選択公理を仮定すると、完全加法性を満たさない例が作れる。（40ページ）
    • 相異なる任意の2つの集合の距離が正となる集合族では、ルベーグ外測度の完全加法性が成り立つ。（定理3.3）

2つの可測性の関係

リーマン積分と2つの方式の面積の関係

  • リーマン積分の定義は46〜47ページ参照。
  • 閉区間上でリーマン積分可能な関数について、x軸と閉区間上のグラフが囲む領域はルベーグ可測であり、その領域の定積分とルベーグ測度は一致する。（定理3.7）
  • 言い方を変えると、リーマン積分で求められない図形の面積がルベーグ積分で求められる可能性がある。


どんな集合がルベーグ可測集合か？ *1

  • 空集合、全体集合
  • 閉集合
    • 有限の場合：定理3.9、一般の場合：系3.9'
  • 開集合
    • 有限の場合：系3.15（平面の2進分解と2進正方形を使う）、一般の場合：系3.15'
  • 可算個のルベーグ可測集合の和集合と共通部分
  • ルベーグ可測集合の補集合
    • 上の2つは定理4.1より。また、差集合も同様。
  • 等測包 *2 と零集合による特徴付け（系4.4）
    • 等測包と等測核 *3 の差を零集合にできることがポイント（系4.3）
    • 定理3.16'を使って証明する。


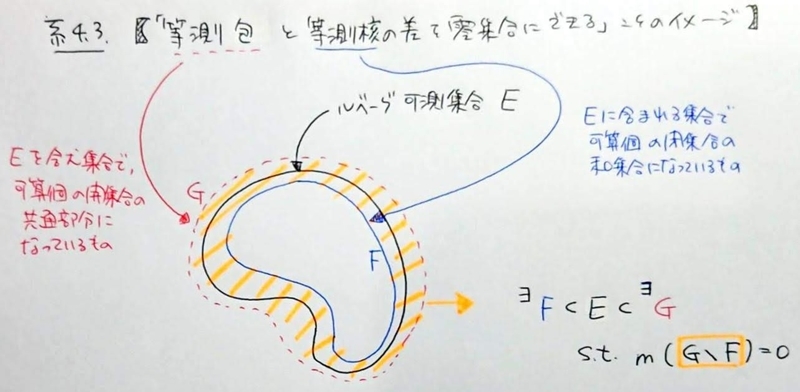
ルベーグ測度の計算

  • 差集合のルベーグ測度の計算（系4.2）
  • 包含関係について単調性を持つ集合族が収束する集合のルベーグ測度を極限値で求める。（定理4.5）
  • ルベーグ測度は平行移動・裏返し・回転に関して不変である。（定理4.8～4.10）

その他：補題3.8の証明の補足

  • 49ページの証明3行目：定理A.10を使う。
  • 50ページの上から2行目：収束列がコーシー列であることを使う。

*1:ルベーグ可測集合は定義3.18で定義されている。

*2:等測包：ルベーグ可測集合を含む、ある開集合たちの共通部分

*3:等測核：ルベーグ可測集合に含まれる、ある閉集合たちの和集合

ジョルダンとルベーグの面積の定義〜『ルベーグ積分講義』読書メモ

数学 読書メモ

ルベーグ積分に再入門したいということで、『ルベーグ積分講義』（新井仁之 著）を読んでいます。

ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち

ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち

堅くもないけど多少の骨がありそうなこの本に行き着きました。

現時点で読み終えた第6章までの印象では、ほとんど行間がなくとても読みやすい本です。
頭の中で計算を追える程度に詳しく書かれています。

この本の読書メモ第1回として、第1〜2章についてまとめます。

なお、わかりやすさとイメージを優先して、この記事では「面積」という用語を正しく使っていない部分もありますので、ご注意ください。

2つの方式の面積の定義

「そもそも図形の面積とは何か？」からスタートして、

が書かれています。

ジョルダン方式は、有界であまり複雑ではない図形の面積を測定できます。

一方、ルベーグ形式は、有界に限らない複雑な図形の面積を測定することができます。

ルベーグ形式はジョルダン形式より精密に面積を測定でき、両者で測定した面積が同じ値になることが、第3章で述べられています。

2つの方式の比較

2つの方式の詳細は本文参照としますが、両者を比較すると次のように整理できます。


その他のメモ

  • 第1章を読む前に、付録A（実数の基本的な性質）と付録D（可算集合）を読んでおくとよい。
  • PDFの[注1]にある基本長方形での定義の仕方が、もともとのジョルダンの定義の仕方である。
  • 第2章を読む前に、この章でよく使われる問題2.1の主張を頭に入れておくとよい。
  • 定理2.8で述べられている性質は、位相空間論でコンパクトと呼ばれる。

読むタイミングがぴったりだった！ ～ 『仕事論』読書メモ

水曜どうでしょう 読書メモ

私は『水曜どうでしょう』の初期からのファンで、DVD全巻購入はもちろん、出演者の著作もなるべく読むようにしています。

しかし、藤村Dと嬉野Dの本『仕事論』は、すぐに読もうという気にはなれませんでした。

仕事論

仕事論


というのも、メンタル不調による休職中で、ビジネス書からは意識的に距離をとっていたため。不調のときにビジネス書を読むと気分が落ち込むことが経験的にわかっていたからです。

『仕事論』というタイトルが、ストレートにビジネス書然としていて、意識的に避けていました。


しかし、リワーク（復職支援プログラム）の受講が終了し、職場復帰の意欲が出てきました。

何気なく書店で手に取ってパラパラめくると、「読めるかもしれない」と思い、勢いで購入しました。


番組のことをよく知っているせいか、すらすら読むことができました。


ざっくりまとめると、この本には次の3つが書かれていると考えています。

前半（第1～2章）
組織（会社）で働くということ
中盤（第3～5章）
仕事をする上で、自分の意志を持つことが大事
後半（第6章）
自分の人生における仕事の位置づけ


前半は、組織で働くことについての2人の強力な思いが書かれていて、メンタルが弱っているときだとかえって追い詰められて、この先を読むのをあきらめたと思います。

正論であり筋が通っているだけに、非常に強力な思いがあふれていて圧倒されました。


中盤は、これまでの自分の仕事の中でできなかったことを、改めて思い起こさせてくれました。

もうすぐ来る復職の後は、自分の意志を持って仕事ができるようにしたいものです。


後半は、書かれている内容が自分の理想に近いという印象を持ちました。

『水曜どうでしょう』でやっていることはその理想を貫き通しているように見える。
しかし、実際問題、多くの人にとって理想通りに生きるのは難しい。
だから、この番組のような生き方にみんなが憧れて、これほど支持を受けているのだと感じました。

この理想は、DVD副音声の中で繰り返し語られています。（以下の記事でまとめています）

wed7931.hatenablog.com


全体を通して思うのは、メンタル不調から立ち直りつつある現時点で読むのがぴったりな本だったということです。

道に迷いそうになったときには、また読み返したいと思います。