ルベーグ測度の性質〜『ルベーグ積分講義』読書メモ
前回の読書メモでは、ジョルダンとルベーグの2つの方式での面積の定義について整理しました。
今回は、第3〜4章に書かれているルベーグ測度の性質をまとめます。
第3〜4章を読む上で注意すること
2つの加法性
2つの可測性の関係
リーマン積分と2つの方式の面積の関係
- リーマン積分の定義は46〜47ページ参照。
- 閉区間上でリーマン積分可能な関数について、x軸と閉区間上のグラフが囲む領域はルベーグ可測であり、その領域の定積分とルベーグ測度は一致する。(定理3.7)
- 言い方を変えると、リーマン積分で求められない図形の面積がルベーグ積分で求められる可能性がある。

どんな集合がルベーグ可測集合か? *1
- 空集合、全体集合
- 閉集合
- 有限の場合:定理3.9、一般の場合:系3.9'
- 開集合
- 有限の場合:系3.15(平面の2進分解と2進正方形を使う)、一般の場合:系3.15'
- 可算個のルベーグ可測集合の和集合と共通部分
- ルベーグ可測集合の補集合
- 上の2つは定理4.1より。また、差集合も同様。
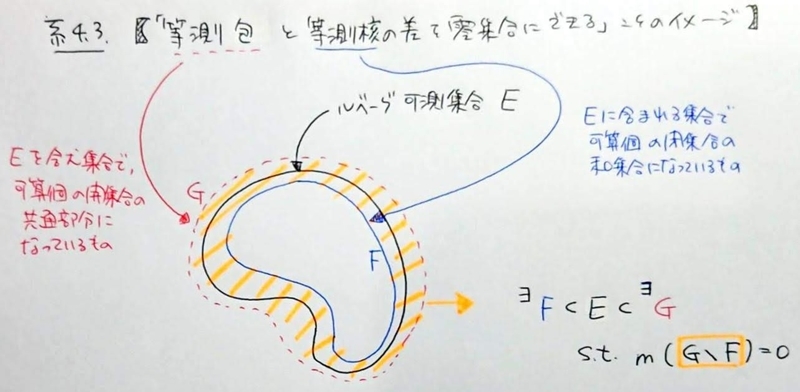
- 等測包 *2 と零集合による特徴付け(系4.4)
- 等測包と等測核 *3 の差を零集合にできることがポイント(系4.3)
- 定理3.16'を使って証明する。
ルベーグ測度の計算
その他:補題3.8の証明の補足
- 49ページの証明3行目:定理A.10を使う。
- 50ページの上から2行目:収束列がコーシー列であることを使う。
