7931のあたまんなか

数学／読書メモ／自分の考え方／水曜どうでしょう／交通関係（道路・航空）など、頭の中にあることを書き出しています。

d次元ルベーグ測度～『ルベーグ積分講義』読書メモ

数学 読書メモ

『ルベーグ積分講義』（新井仁之 著）の読書メモ第4回です。

ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち

ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち

第Ⅰ部「面積とは何か」の最後のまとめです。

これまでの読書メモはこちらです。

今回は第6章「d次元ルベーグ測度」のまとめです。

一般の次元のルベーグ測度

第5章までで議論されてきた2次元実数空間 \mathbb{R}^2 のルベーグ測度を拡張して、第6章では一般の d 次元実数空間 \mathbb{R}^d のルベーグ測度を定義します (d = 1,2,\dots) 。

2次元で成立する各命題は、 d 次元でも同様に成立することが説明されています。

第6章の主張と第1～5章の主張の対応

第6章で説明されているいろいろな定義や定理は、第1～5章の定義や定理に対応しており、証明も同様にできます。

ここではその対応をまとめます。

第6章の主張 対応する第1～5章の主張 備考
定義6.1 定義1.2 基本直方体、基本立方体
定義6.2 定義2.1 ルベーグ外測度
定理6.3 定理2.16
定理6.4 定理3.2 ルベーグ外測度の劣加法性
定義6.5 例2.2 （有界）閉集合
定義6.6 定義2.7 ルベーグ内測度
定義6.7 定義2.10, 定義3.18 ルベーグ可測集合、ルベーグ測度
定義6.8 定義3.10 開集合
定理6.9 定理3.16'
開集合はルベーグ可測 系3.15'
閉集合はルベーグ可測 系3.9'
定理6.10 (1) 定理4.1
定理6.10 (2) 定理3.1' ルベーグ測度の完全加法性
定理6.11 (2)の条件 定義5.1 カラテオドリの可測性
定理6.11 定理5.5 ルベーグ可測とカラテオドリ可測が同値
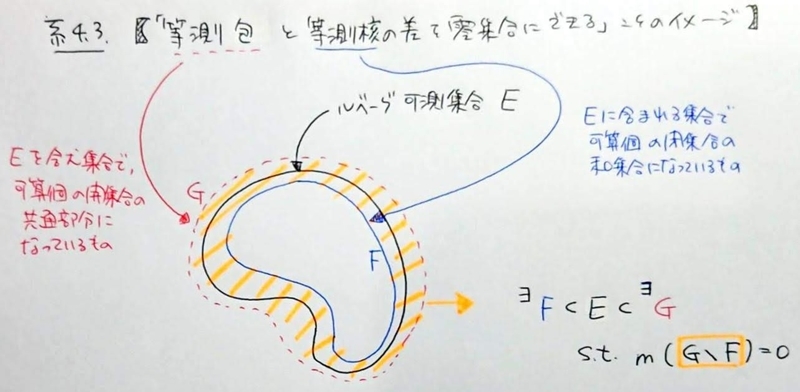
系6.12 系4.3 等測核、等測核
定義6.13 命題2.11 (2) 零集合
系6.14 系4.4
定理6.15 定理4.5

カラテオドリの意味での可測性～『ルベーグ積分講義』読書メモ

数学 読書メモ

『ルベーグ積分講義』（新井仁之 著）の読書メモ第3回です。

ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち

ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち

Amazon

これまでの読書メモでは、 ジョルダンとルベーグの2つの方式での面積の定義 と ルベーグ測度の性質 について整理しました。

今回は第5章のまとめです。

カラテオドリによるルベーグ可測性の特徴づけ

上にあるこの節の見出しは、第5章のタイトルそのものにしました。

第2章で定義されたルベーグ可測性と同値なものとして、カラテオドリによる可測性の定義があることが、この章を通じて説明・証明されています。

ルベーグ測度は「ルベーグ外測度＝ルベーグ内測度」で定義されました。

カラテオドリの意味で可測であることは、ルベーグ外測度のみで記述されます。（定義5.1）

これまでに説明されているジョルダン可測性やリーマン可積分性との関係をまとめると、次のような図で表現できます。


補足

命題5.1について

  • 主張：定理4.1との類似性に注目する。
    • 定理4.1の \mathfrak{M} を \mathfrak{M}^* に置き換えたものが命題5.1の主張である。
  • 証明：定理4.1の位相空間論を使った証明とは異なる。

定理5.5の証明

  • 81ページ6行目：定理3.1'を使う。
  • 81ページ8～9行目：開集合 G と集合 G \cup A, \ G \cap A^c はルベーグ可測であること（系3.15と定理4.1より）と定理3.1'より、8行目の最右辺を得る。また、ルベーグ可測集合 B に対して m(B) = m^* (B) であることと E \cap A \subset G \cap A 、および補題2.9より、9行目を得る。
  • (2)⇒(1)の証明で開集合 G と U をとれる理由：補題3.17の(i)と(ii)を繰り返し適用すればよい。
  • (2)⇒(1)の m^*(A) = \infty の場合の証明の結末： A_n がルベーグ可測であることと A= \bigcup_{n=1}^{\infty} A_n および定理4.1 (4)から、 A がルベーグ可測になる。

ルベーグ測度の性質〜『ルベーグ積分講義』読書メモ

数学 読書メモ

『ルベーグ積分講義』（新井仁之 著）の読書メモ第2回です。

ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち

ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち

Amazon

前回の読書メモでは、ジョルダンとルベーグの2つの方式での面積の定義について整理しました。

wed7931.hatenablog.com

今回は、第3〜4章に書かれているルベーグ測度の性質をまとめます。

第3〜4章を読む上で注意すること

  • 各主張がルベーグ測度 or ルベーグ外測度のどちらに関することか？
  • ルベーグ測度が有限 or 一般の場合（有限とは限らない）か？
    • 全般的に、前半で有限の場合、後半で一般の場合を示している。

2つの加法性

  • ルベーグ測度は完全加法性（または σ-加法性）を持つ。
    • 有限の場合：定理3.1、一般の場合：定理3.1’
  • ルベーグ外測度は劣加法性を持つ。
    • 一般の場合：定理3.2（有限の場合を含む）
  • ルベーグ外測度が完全加法性を満たすかは難しい問題
    • 選択公理を仮定すると、完全加法性を満たさない例が作れる。（40ページ）
    • 相異なる任意の2つの集合の距離が正となる集合族では、ルベーグ外測度の完全加法性が成り立つ。（定理3.3）

2つの可測性の関係

リーマン積分と2つの方式の面積の関係

  • リーマン積分の定義は46〜47ページ参照。
  • 閉区間上でリーマン積分可能な関数について、x軸と閉区間上のグラフが囲む領域はルベーグ可測であり、その領域の定積分とルベーグ測度は一致する。（定理3.7）
  • 言い方を変えると、リーマン積分で求められない図形の面積がルベーグ積分で求められる可能性がある。


どんな集合がルベーグ可測集合か？ *1

  • 空集合、全体集合
  • 閉集合
    • 有限の場合：定理3.9、一般の場合：系3.9'
  • 開集合
    • 有限の場合：系3.15（平面の2進分解と2進正方形を使う）、一般の場合：系3.15'
  • 可算個のルベーグ可測集合の和集合と共通部分
  • ルベーグ可測集合の補集合
    • 上の2つは定理4.1より。また、差集合も同様。
  • 等測包 *2 と零集合による特徴付け（系4.4）
    • 等測包と等測核 *3 の差を零集合にできることがポイント（系4.3）
    • 定理3.16'を使って証明する。


ルベーグ測度の計算

  • 差集合のルベーグ測度の計算（系4.2）
  • 包含関係について単調性を持つ集合族が収束する集合のルベーグ測度を極限値で求める。（定理4.5）
  • ルベーグ測度は平行移動・裏返し・回転に関して不変である。（定理4.8～4.10）

その他：補題3.8の証明の補足

  • 49ページの証明3行目：定理A.10を使う。
  • 50ページの上から2行目：収束列がコーシー列であることを使う。

*1:ルベーグ可測集合は定義3.18で定義されている。

*2:等測包：ルベーグ可測集合を含む、ある開集合たちの共通部分

*3:等測核：ルベーグ可測集合に含まれる、ある閉集合たちの和集合

ジョルダンとルベーグの面積の定義〜『ルベーグ積分講義』読書メモ

数学 読書メモ

ルベーグ積分に再入門したいということで、『ルベーグ積分講義』（新井仁之 著）を読んでいます。

ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち

ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち

堅くもないけど多少の骨がありそうなこの本に行き着きました。

現時点で読み終えた第6章までの印象では、ほとんど行間がなくとても読みやすい本です。
頭の中で計算を追える程度に詳しく書かれています。

この本の読書メモ第1回として、第1〜2章についてまとめます。

なお、わかりやすさとイメージを優先して、この記事では「面積」という用語を正しく使っていない部分もありますので、ご注意ください。

2つの方式の面積の定義

「そもそも図形の面積とは何か？」からスタートして、

が書かれています。

ジョルダン方式は、有界であまり複雑ではない図形の面積を測定できます。

一方、ルベーグ形式は、有界に限らない複雑な図形の面積を測定することができます。

ルベーグ形式はジョルダン形式より精密に面積を測定でき、両者で測定した面積が同じ値になることが、第3章で述べられています。

2つの方式の比較

2つの方式の詳細は本文参照としますが、両者を比較すると次のように整理できます。


その他のメモ

  • 第1章を読む前に、付録A（実数の基本的な性質）と付録D（可算集合）を読んでおくとよい。
  • PDFの[注1]にある基本長方形での定義の仕方が、もともとのジョルダンの定義の仕方である。
  • 第2章を読む前に、この章でよく使われる問題2.1の主張を頭に入れておくとよい。
  • 定理2.8で述べられている性質は、位相空間論でコンパクトと呼ばれる。

読むタイミングがぴったりだった！ ～ 『仕事論』読書メモ

水曜どうでしょう 読書メモ

私は『水曜どうでしょう』の初期からのファンで、DVD全巻購入はもちろん、出演者の著作もなるべく読むようにしています。

しかし、藤村Dと嬉野Dの本『仕事論』は、すぐに読もうという気にはなれませんでした。

仕事論

仕事論


というのも、メンタル不調による休職中で、ビジネス書からは意識的に距離をとっていたため。不調のときにビジネス書を読むと気分が落ち込むことが経験的にわかっていたからです。

『仕事論』というタイトルが、ストレートにビジネス書然としていて、意識的に避けていました。


しかし、リワーク（復職支援プログラム）の受講が終了し、職場復帰の意欲が出てきました。

何気なく書店で手に取ってパラパラめくると、「読めるかもしれない」と思い、勢いで購入しました。


番組のことをよく知っているせいか、すらすら読むことができました。


ざっくりまとめると、この本には次の3つが書かれていると考えています。

前半（第1～2章）
組織（会社）で働くということ
中盤（第3～5章）
仕事をする上で、自分の意志を持つことが大事
後半（第6章）
自分の人生における仕事の位置づけ


前半は、組織で働くことについての2人の強力な思いが書かれていて、メンタルが弱っているときだとかえって追い詰められて、この先を読むのをあきらめたと思います。

正論であり筋が通っているだけに、非常に強力な思いがあふれていて圧倒されました。


中盤は、これまでの自分の仕事の中でできなかったことを、改めて思い起こさせてくれました。

もうすぐ来る復職の後は、自分の意志を持って仕事ができるようにしたいものです。


後半は、書かれている内容が自分の理想に近いという印象を持ちました。

『水曜どうでしょう』でやっていることはその理想を貫き通しているように見える。
しかし、実際問題、多くの人にとって理想通りに生きるのは難しい。
だから、この番組のような生き方にみんなが憧れて、これほど支持を受けているのだと感じました。

この理想は、DVD副音声の中で繰り返し語られています。（以下の記事でまとめています）

wed7931.hatenablog.com


全体を通して思うのは、メンタル不調から立ち直りつつある現時点で読むのがぴったりな本だったということです。

道に迷いそうになったときには、また読み返したいと思います。

特集「ひろがりゆく可積分系の世界」～『数学セミナー2019年3月号』読書メモ

数学 数学セミナー 本 読書メモ

『数学セミナー 2019年3月号』の特集は「ひろがりゆく可積分系の世界」です。

数学セミナー 2019年 03 月号 [雑誌]

数学セミナー 2019年 03 月号 [雑誌]

私にとって、可積分系という言葉は聞いたことがある程度でした。

5つの記事を読んでいく中で、数学だけでなく物理や生物など他分野との関係が広がっていることがわかりました。

そして、私がこれまでに読んだ本の中でも触れられていた概念であることに気付かされました。

諸科学に飛び出す可積分系

前半は可積分系の定義とその数学的な例、後半は他分野へ波及している内容が書かれています。

「微分方程式は通常は解けないもの」 *1 だというのが出発点です。

可積分系の定義

本文では「厳密な定義がない」と断りを入れた上で、次のように記載されています。

本来は解けないはずの非線形微分方程式や差分方程式などが，ある意味で厳密に解け，さまざまなよい構造が付随するとき，それらの方程式を可積分系と呼ぶことが多い．（8ページより引用）

「よい構造」として5つが挙げられており、それぞれについて代表的な方程式や解が例示されています。

例えば、KdV方程式、サイン・ゴルドン方程式、戸田格子方程式、ソリトン解などです。

特に、ソリトンは粒子のような振る舞いを見せる孤立波として、この特集では何度も出てきます。 *2

また、従属変数の変数変換や、微分方程式の離散化による差分方程式の導出などがよく使われる方法のようです。

越境する可積分系：数理モデルとアルゴリズム

まずは、可積分系とそれを解くアルゴリズムの関連性を以下の例で説明しています。

次に、非線形シュレディンガー方程式 *4 や短パルス方程式を例に、可積分性や解の構造を崩さずに離散化する方法が書かれています。

最後に、ローグ波と呼ばれる海洋に突然現れる巨大な波の研究について触れられています。

箱玉系の広がり

箱玉系について、「浅水波を記述するKdV方程式の特徴であるソリトン現象に注目し，箱と玉のみからなる系に対する単純なルールとして抽出したもの」 *5 と説明されています。

力学系やオートマトン、確率論などへの広がりを持つ概念として、具体例を多く交えて書かれています。

書かれている内容を実際に手を動かして計算すると、簡単なパズルをやっているようで楽しい気持ちになりました。

この記事を読み進めながら「箱玉系やオートマトンの図をどこかで見たことがある」と思って調べてみると、10年以上前に読んだ『渋滞学』（西成活裕）に同じような図が出てきていました。

渋滞学 (新潮選書)

渋滞学 (新潮選書)

粘菌とソリトン

粘菌というと、イグノーベル賞を受賞した迷路を解く研究がまず思い浮かびますが、ソリトンのような挙動を示す生物としても注目されています。

これは、それを研究する生物学者による記事です。

数式は全く出てこず、粘菌のソリトンのような動きを表す写真が多く登場し、見ているだけでおもしろくて不思議な気持ちになります。

工業デザインと可積分系

工業デザインに出てくる“美しい”とか“魅力的”とされる曲線を定式化する取り組みを行ったところ、ソリトンや可積分性の性質が現れたというお話です。

対数型美的曲線や準美的曲線など、「美的」という言葉が入る不思議な数学用語（？）も出てきます。

曲率、相似幾何 *6 、リッカチ方程式、弾性曲線などの概念が出てきます。

ちょっと寄り道：クロソイド（緩和曲線）

本筋とは離れますが、道路の曲線設計で使われるクロソイド（緩和曲線）がちらりと説明されています。

道路設計でなぜこれが出てくるかがずっと疑問でしたが、この記事を読んで「ハンドルを切る＝曲率を連続的に変化させる」と解釈すると合点がいきました。

*1:8ページより引用

*2:私にとって最もわかりやすいソリトンの説明は、25ページにありました。

*3:行列の固有値を計算するアルゴリズムの1つ

*4:式に出てくるローマン体の i は虚数単位を表します。

*5:17ページより引用

*6:《大まかに言えば，ユークリッド幾何では「直線」を基準とし曲線の曲がり具合を表現しているが，相似幾何では円を基準にしているのである．》（30ページより引用）

連載「試験のゆめ・数理のうつつ」 ～ 『数学セミナー』読書メモ

数学セミナー 数学 読書メモ

『数学セミナー』では、2017年4月号から、時枝正さんによる「試験のゆめ・数理のうつつ」が連載されています。

数学セミナー2017年4月号 数学の学び方

数学セミナー2017年4月号 数学の学び方

いろいろな分野の重要定理やそれを使った問題を俯瞰できる連載で、とても気に入っています。
各月でどのような内容が紹介されているかを記録するのが、この記事の目的です。

この連載の概要

ケンブリッジ大学の数学専攻の試験にトライポスというものがあります。

この連載では、各月のテーマごとにトライポスの雰囲気を感じられる問題が紹介されています。

各月で紹介される問題は10問前後で、簡潔な解答がつけられています。

複数分野が融合された問題も見られ、意外な発見があるのが楽しみです。

【第1回 - 2017年4月号】ケンブリッヂの入試

イントロダクションとして、ケンブリッジの数学専攻に入るための口頭試験のサンプル問題が紹介されています。

「口頭」と言いながらも、このような試験のようです。

座るやいなや，問題を与える．「口頭」とは名ばかり，その場でペンと紙をどしどし使わせ，つまづくようす，解くようす，あきらめるようす，巻き返すようす，を観察する．すぐ解けるようなら問題を難しくし，なかなか解けぬようなら易しくし，初めの2～3分でその人がこなせるぎりぎりの水準を探り当て，30分間6つ～7つ問題をやらせるのである．
（『数学セミナー 2017年4月号』45ページより引用）

紹介されている12問から2問を引用します。

問3　100! のしっぽにはいくつ 0 が連なるか？

問6　すべすべな面に静止したおはじきAに，同質量のおはじきBをぶつけると，散乱角は 90° になる．これを導け．正面衝突させると何がおこるか？

【第2回 - 2017年5月号】確率：逆説あれこれ，条件付けて考える

一般的な確率の問題から、標本調査、ベイズ統計、条件付確率／期待値、幾何確率、積分確率などに関する問題が紹介されています。

印象的だったものは、 調和平均 ≦ 幾何平均 ≦ 算術平均 の関係を確率論的にとらえた問題（題5）です。

確率や期待値を積分を使って評価する問題もいくつかあります。
あまりやったことがないので、とても新鮮に見えました。

【第3回 - 2017年6月号】力学：保存量やりとり，次元解析

運動量、遠心力、ケプラーの三法則、エネルギーなど、数学というより物理の内容です。

高校物理＋αしか学んでいない私にとって、新鮮味がある問題ばかりでした。

例えば、こんな問題。

題5　片面バターを塗ったトーストがテーブルの縁から落ちると，えてしてバター面がうつぶせに着地しますよね．くるりとフル回転してあおむけに着地させるためにはテーブルの高さを何倍にすべきか？即答しなさい．

題8　川床にグラフ B=B(x) で与えられるこぶを築いたとき，川面の高低はどう変わるか？

【第4回 - 2017年7月号】群：対称性をみぬき，作用してほぐす

タイトルにあるとおり、群の作用に着目した問題が紹介されています。

問題に対する解答の帰結として、基本群の例やフェルマーの小定理が得られる問題もあります。

考えたことがなかった！と思ったのが、次の2つの問題です。

題7　群から2元をランダムに抽出したとき，それらが可換な確率は何か？

（題8の後に書かれた内容の抜粋）
群，群というけれど，群ってありふれた存在なのでしょうか？それとも稀なのかな？
定理 位数 n の群の数は高々 n!^{\log_2 n} である。
―結合律はかくも厳しい要請なのであった。

【第5回 - 2017年8月号】1変数の微積分：テレスコープ原理，連続と離散

この回は、以下の3つの部分に分類されます。

ディガンマ関数とは、ガンマ関数の対数微分を取ったものとのこと。

ガンマ関数が乗法的とすると、ディガンマ関数は加法的と考えられ、無限級数との相性がよさそうです。

余談ですが、「連続と離散」というと、微分・積分と差分・和分の関係を初めて知った『数学ガール』を読んだときの衝撃が印象に残っています。

数学ガール (数学ガールシリーズ 1)

数学ガール (数学ガールシリーズ 1)

この連載と同じく『数学セミナー』で連載中の梅田亨さんの「計算するたのしみ―スターリング数のいる風景」でも、差分・和分が扱われており、いずれじっくり読んでみたいと思っています。

【第6回 - 2017年9月号】ベクトル解析：ラプラシアンの意味，球の調和場

前半は調和関数（ラプラス方程式 \triangle \varphi = 0 の解）に関する問題が紹介されています。

後半はベクトル解析を使って、重力ポテンシャルなどの話が出てきます。
（後半の内容は知識がほとんどないので、私の力では説明できません…）

調和関数は、私の修士時代の研究内容に関係してきます。
時間があれば、改めて勉強したいと思っています。

印象に残った次の問題は、複素関数論のリュウビルの定理の一般化とのこと。
具体的にどういう関係なんだろう？

題8　 \mathbb{R}^n 全体で有界な調和関数は定数である。

【第7回 - 2018年4月号】数論：素数のたちい，合同式のふるまい

6ヶ月間の休載を経て、次は素数と合同式の話題です。
学部時代に勉強した内容でとても懐かしい思いがしました。

内容は次のように分類されます。

素数定理を使った次の問題が印象的です。（本文と記述は変えています）

題17　素数/素数の形の有理数全体は、正の実数全体の集合で稠密である。*3

【第8回 - 2018年5月号】微分方程式：デルタとグリーン，指数函数百面相

微分方程式の解をグリーン関数と呼ばれる関数で記述する問題などが出てきます。

グリーン関数は初めて知りました。ディラックのデルタ関数で記述する関数です。

ですので、たたみ込みやフーリエ変換がからむ話も出てきます。先日書いたこの記事の続きにあたる内容です。（続きを書きたいけど、手が出てません）
wed7931.hatenablog.com

ほかにも、調和振動、強制減衰振動、うなり、共鳴、シュレディンガー方程式、特異摂動といった物理関係の話題が出てきます。

【第9回 - 2018年6月号】確率：エントロピーでえらび，母函数できわめる

前半はエントロピーと確率の関係、後半はまさに確率に関する話です。

…が、今回は畑違いすぎてお手上げです。エントロピーは学部1年の物理の講義で聞いたことがあるなぁという程度です。

解答の内容は理解できませんでしたが、おもしろそうな問題を2つ挙げておきます。

題5　塩漬・糖漬が食品を長持ちさせるのはなぜか？

題11　1990年代GPSは軍事用チャネルと民間用チャネルが併存し，米国防省はわざと雑音を混ぜて民の精度を落としていた．ところが，あっけない工夫のおかげで，民のみ受信してなお軍の精度を達成する人が続出したので，雑音を廃した，という伝説がある．どんな工夫だったでしょうか？

キーワード：ボルツマン分布、確率変数の列の収束の概念いろいろ、大数の法則と中心極限定理の証明、ワイエルシュトラスの近似定理など

【第10回 - 2018年7月号】力学：まわる剛体，いたずらな接点

タイトルにあるように、剛体の力学がテーマです。

自分でも多少は理解できたので、高校程度の物理の知識（慣性モーメント、摩擦係数、回転運動など）があればざっと読めるかと思います。

扱われている問題も生活に即したものが多く、イメージしやすく楽しいです。

  • 氷上の回転椅子に座って回転するには？（題1）
  • 長さが同じ4本脚の机を床に置くと、ガタガタすることがあるのはなぜか？それを直すにはどうすればいいか？（題2）
  • ビリヤード玉にバックスピンやトップスピンをかけるにはどこを打つべきか？（題8）
  • 逆立ち独楽はなぜ逆立ちするか？（題11）

【第11回 - 2018年8月号】群：位数をよりあわせ，構造をつむぐ

第4回（2017年7月号）に続いて、「群」は2回目です。

前半はあみだくじに代表される対称群と置換の符号について。

n 次対称群 S_n と交代群 A_n の生成系、正多面体群と同型な群などがまとめられています。

次の問題は初めて見ました。確率と期待値を使って解かれています。

題5　 S_n の置換の転倒数の平均は \frac{1}{2} \binom{n}{2} = \frac{n(n-1)}{4} 。

記事内で言及されている15パズルの可解性は、『数学セミナー 2017年10月号』で取り上げられています。

wed7931.hatenablog.com

後半は元の位数に関する問題です。

印象的なのはこの問題です。

題8　 S_9 に位数20の元は存在するか？位数18の元はどうか？ S_n の元の最大位数はどのくらいか，みつもれ．

最後には、スピンの実験が説明されています。群の準同型と2重被覆、ホモトピー類を体現する実験とのこと。 *4

【第12回 - 2018年9月号】線形代数：自由度の勘定，行列の分解

ガウスの消去法や次元定理などの線形代数の基本から、ラグランジュ補完、ホモロジー、離散フーリエ変換などの話題に展開していきます。

線形代数の教科書でよく見る問題が多い中、次の2つの問題が印象的です。前者は計算量、後者は固有値に関する問題。

題3　四則演算を1ステップと数えて，未知数 n 個，式 n 本の消去法のコストをみつもれ．クラメールの規則と比べよ．

題14　一年中雨季のケンブリッヂでは， k 日目の降水量 r_k を \frac{r_{k-3} + r_{k-2} + r_{k-1} }{3} と予報する． r_1, r_2, r_3 は天気予報史初期の観測値，三日坊主で以来観測はやめてしまった．この数列は収束するか？収束先の極限は？

【第13回 - 2018年10月号】多変数微積分：渦巻く場，秘法 εε=δδ-δδ

前半はラグランジュ乗数やヘッセ行列、ストークスの公式などが扱われています。

後半はベクトル積とナブラ \nabla の関係式と物理との関係です。ビオ-サバールの法則、マクスウェル方程式、ナビエ-ストークス方程式など、物理関係の用語が並びます。

次の問題は一見とっつきにくいですが、解答を見て「なるほど！」と思いました。

題5　閉多角形各辺にその辺のサイズの外向き垂ベクトル \mathbf{n}_i を植える． \sum_{i} \mathbf{n}_i = 0 である（各 \mathbf{n}_i を90°捻った和は閉 =0．捻る前の和も =0）．閉多面体の類似はいかに？アルキメデスの浮力を説明しなさい．

【第14回 - 2018年11月号】集合：明るい形式，無限の暗がり

数学的帰納法、集合の基数（濃度）、選択公理・整列定理・ツォルンの補題の同値性など。

松坂和夫『集合・位相入門』で勉強していた内容を、とてもざっくりと復習した感じです。

印象的なのは次の問題です。ここで、可算無限 \aleph_0 = | \mathbb{N} | と連続体の濃度 \mathfrak{c} = \aleph= | \mathbb{R} | です。

題4　 \mathbb{R} から \mathbb{R} への解析関数全体の基数を言え．（文言を変えています）

題5　連続関数 f: \mathbb{R} \to \mathbb{R} で，有理数では無理値を，無理点では有理値を取るものは存在するか？存在するなら例を作り，しないなら理屈を説明せよ．

\mathbb{Q} 上 \mathfrak{c} 次元ベクトル空間 \mathbb{R} の基底の存在（解8の文中）

加えて、あまりなじみのないシュペルナー族やランダムグラフ（とベッチ数の関係）についても書かれています。

【第15回 - 2018年12月号】微分方程式：軌道のゆくえ，相図のかわりめ

常微分方程式の解軌道、平衡点（不動点）の安定性と分岐、微分方程式を離散化した差分方程式、力学系など。

後半は物理に関係する話題が出てきます（減衰ふりこ、勾配流、シュレディンガー方程式など）。

常微分方程式はほとんど理解できていないため、うまくレポートできないのが残念です…。

【第16回 - 2019年1月号】確率：分枝と乱歩，ポワソンと待ち行列

前半は3種類の確率過程（分枝過程、乱歩、連続時間の確率過程）、後半は待ち行列のモデルについて書かれています。

特に、乱歩の確率過程では母関数（離散的な確率分布を係数にした冪級数）が大きな役割を果たしています。

乱歩は 『数学ガール／乱択アルゴリズム』 第8章、母関数は 『数学ガール』 第4章が参考になりそうです。

【第17回 - 2019年2月号】特殊相対論：時空の幾何，4運動量の物理

前半は、特殊相対論の主張やそこから導かれる内容について、ミンコフスキー時空やローレンツ群を使って説明されています。

光円錐やローレンツ群の単位元を含む連結成分 \mathrm{SO}^{+} (1,1) などが出てきて、自分が書いた表現論の修士論文に出てきた！とワクワクしました。
もう一度、きちんと理解したいものです。

後半は、4運動量と呼ばれるものを使って議論が展開されています。
残念ながら、ほとんど理解できませんでした…。

題4に書かれている「光速以下の速度をいくら加えたって光速は超えない」という主張がとても印象的です。

【第18回(最終回) - 2019年3月号】トライポス小史

この連載で扱われたトライポスの歴史が書かれています。

年代が進むにしたがって出題範囲が広くなっていっています。

18世紀の出題範囲にすでに含まれている静水力学という用語を初めて知りました。流体力学があることを考えると自然ですね。

また、後半に書かれている、学生指導についての筆者の工夫が印象的です。

*1:素因数分解をしたときに（1以外の）平方因子を持たない数のこと。つまり、素因数分解が相異なる素数の積になる。

*2:フェルマーの小定理の一般化

*3:つまり、 \alpha < \beta を満たす任意の正の実数 \alpha, \ \beta に対して、 \alpha < p/q < \beta を満たす素数 p, \ q が存在する。

*4:あまり理解できていないです…。