7931のあたまんなか

数学／読書メモ／自分の考え方／水曜どうでしょう／交通関係（道路・航空）など、頭の中にあることを書き出しています。

特集「国際数学者会議2018」～『数学セミナー2019年1月号』読書メモ

数学 数学セミナー 読書メモ

『数学セミナー2019年1月号』の特集は「国際数学者会議2018」です。

数学セミナー 2019年1月号 通巻 687号 国際数学者会議2018

数学セミナー 2019年1月号 通巻 687号 国際数学者会議2018

4年に1度開催される国際数学者会議（ICM）の様子と各賞受賞者の業績が紹介されています。

ICM 2018滞在記

2018年8月1日～9日にブラジル・リオデジャネイロで行われたICMの様子が紹介されています。

その中で、プレナリートークの一覧がまとめられています。

私の興味の対象である表現論に関する講演がいくつかあり、講演内容が気になりました。

フィールズ賞：ビルカー

「ファノ多様体の有界性と極小モデルプログラムへの貢献」について書かれています。

双有理幾何学と呼ばれる分野でのBAB予想に対する貢献のようです。

…残念ながら私の能力では理解できませんでした。

フィールズ賞：フィガッリ

偏微分方程式、幾何、確率論の3分野にまたがる貢献での受賞でした。

私が理解可能なものでは変分問題がこれに含まれ、最適輸送問題や流体運動、シャボン玉の形などに関係します。

冒頭では、最適輸送問題の起こりとなったモンジュ問題が数式を使って説明されており、比較的イメージしやすいものでした。

フィールズ賞：ショルツェ

受賞理由については明確な記述はありませんが、筆者との関係性を中心にショルツェさんの業績を紹介しています。

ポイントとなるキーワードは絶対ガロア群とパーフェクトイド空間のようです。

また、ラングランズ対応についても書かれていて、私の興味対象でもあるので気になっています。

前半では、 p 進数体 \mathbb{Q}_p と位数 p の有限体上の形式ローラン級数体 \mathbb{F}_p ( (t) ) を使って、パーフェクトイド体が説明されています。

これについては、過去に書いたこの記事が参考になりそうです。

wed7931.hatenablog.com

ネヴァリンナ賞：ダスカラキス

受賞理由は「経済的な基本的問題に対する計算複雑度を変えた貢献」と書かれています。

前半はナッシュ均衡計算の困難性、後半はオークションの最適メカニズムの説明です。

個人的には、P vs NP問題の復習から始まっていて、すんなりと読み進めることができました。

また、記事内で最適輸送理論という言葉が出てきており、上述したフィガッリさんの研究との関係を思い起こされました。

ガウス賞：ドノホ

「疎性に着目した情報処理」の観点でドノホさんの業績が説明されています。

議論のスタートは未知変数の個数よりも条件式の個数が少ない連立一次方程式系の話で、数学的議論は比較的易しいように見えます。

数学的内容は置いておいて、次の点がとても印象的でした。

  • この研究が生かされる場面が、医療機器のMRIを例に説明されていてわかりやすい。
  • 現場での発見的手法から出発して、ドノホさんが研究活動に入り込んだ。

チャーン賞：柏原正樹

多くの数学関係のTwitterアカウントで言及された話題で、柏原さんの受賞はよく知っていた。

また、学生時代に表現論を専門にしていたこともあり、柏原さんの名前も知っていた。

実際に、記事の中にはリー群の表現論に関する話題が多く出てきていている。

D加群や量子群の研究者が身近にいたこともあり興味を持っていたが、今は何も知識がないのでいずれ勉強してみたい。

フィールズ賞：ヴェンカテシュ

注：この記事は『数学セミナー 2019年2月号』で書かれていますが、関連性を考慮して本エントリに記載します。（2019/2/3追記）

数論の進展に貢献したとの理由でフィールズ賞を受賞したヴェンカテシュの業績について書かれています。

保型L-関数における問題の概説から始まり、その後のヴェンカテシュの業績の説明では、エルゴード理論やリー群の表現論などの言葉が出てきます。

私が最近読んだエドワード・フレンケル『数学の大統一に挑む』の内容に関係すると思われる部分もあり、個人的にはとても興味深いです。

数学の大統一に挑む

数学の大統一に挑む

また、ヴェンカテシュの論文の特徴が随所に書かれているのが印象的です。例えば、このようなことが書かれています。

具体例によるアフターケアが行き届いているところがヴェンカテシュの論文の特徴である（45ページより引用）
　
ヴェンカテシュの論文にはそういった印象 *1 がほとんどなく，1人でも多くの研究者に自分の研究を理解してもらいたいという気持ちがよく伝わってくる．（48ページより引用）

*1:「分かる人にだけ伝わればよい」というスタンス

Android端末に物理キーボードを接続してみた。

TIPS スマホ

最近、自分のまわりでスマホと物理キーボードをBluetooth接続することが流行っています。

長めの文章を書くために便利かと思い、Amazonで買って使ってみました。

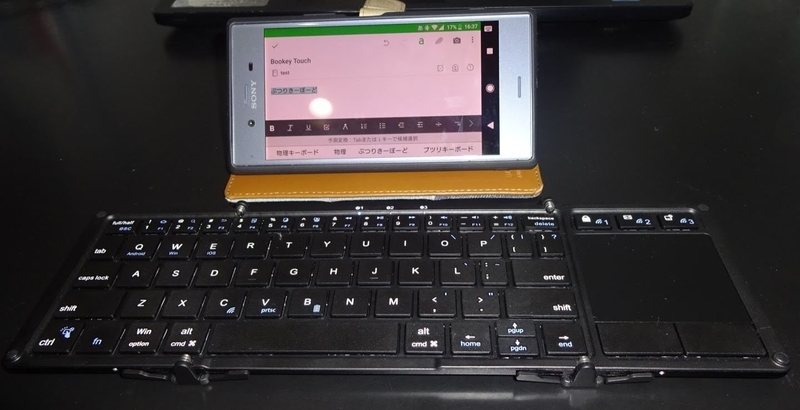
PCのような使い勝手で、スマホで長めの文章を書くのがとても楽で気に入っています。

使うまでに設定周りでちょっとはまったので、メモしておきます。

利用環境

スマホ：Xperia XZ1
OS：Android 8.0.0

物理キーボード：Bookey touch *1

タッチパッド搭載 折りたたみ式 Bluetoothキーボード Bookey touch (ブラック) Android/Windows10/iOS iPhone iPad/Mac対応 ワイヤレス コンパクト 技適取得済 半角/全角キー付 日本語説明書付 JTT Online IPBKYTCBK

タッチパッド搭載 折りたたみ式 Bluetoothキーボード Bookey touch (ブラック) Android/Windows10/iOS iPhone iPad/Mac対応 ワイヤレス コンパクト 技適取得済 半角/全角キー付 日本語説明書付 JTT Online IPBKYTCBK

  • JTT Online
Amazon

Bookey touchの特徴

Bookey touchはタッチパッド付きで、Androidでは画面にマウスカーソルが出てきて、PCと同じようなマウス操作ができます。 *2

そして、マウス操作と画面タッチ操作が併用可能なのが意外と便利です。

スマホと物理キーボードの接続は簡単

スマホと物理キーボードはBluetoothで接続されます。

Bluetoothに慣れていなくても、付属マニュアルを読めば、簡単に接続できます。

物理キーボード設定は「標準キーボード」

使う上でいちばんてこずったのは、物理キーボード設定です。

スマホと物理キーボードを接続した状態で、[設定] - [システム] - [言語と入力] - [物理キーボード] で設定できます。

POBox PlusやGoogle日本語入力やATOKなど、インストールされている日本語変換ソフトが出てきます。

使用したい日本語変換ソフトを選択して、「標準キーボード」に設定します。

こうすることで、次のようなことができます。

  • full/halfキーで、全角／半角入力の切り替え（Windowsと同じ）
  • キーに刻印されたとおりの文字入力 *3

「日本語」に設定しない方がよさそう

「日本語」に設定すると、日本語変換ソフトによって次のようなことが起こりました。

  • full/halfキーで全角／半角入力の切り替えができない。 *4
  • キーに刻印されたとおりの文字入力ができない。
    • 例：キーには「Shift + 2」で「@」が入力できるように刻印されていますが、実際にはWindowsと同様に「"」が入力されます。

なので、キーに刻印されたとおりの入力をするには、「日本語」に設定しない方がよさそうです。

Windowsと同じようなコピペ操作やUNDOができる。

タッチ操作でのコピペやUNDOはやや手間がかかります。

物理キーボードを使うと、「Ctrl + C」でコピーしたり、「Ctrl + Z」でUNDOできたりと、Windowsと同じショートカットキーで操作ができます。

他にもWindowsと同じショートカットキーが使えるようです。

ノートPCを持ち運ぶ必要がなくなった！

長めの文章を書くためにノートPCを持ち運ぶことがありましたが、今後はこのようなことはなくなりそうです。

スマホの小さな画面でも、横画面にすれば長文を打つことにつらさを感じませんでした。

スマホ＋物理キーボード、おすすめです！

*1:2019年1月時点でのAmazonでの価格は5000円程度。

*2:iOSでは、仕様上マウス操作はできないようです。

*3:ただし、「`」と「～」は刻印通りに入力できないようです。

*4:Shift+Ctrlなどで可能。マニュアルに書いてあります。

原子・分子と表現論の関係を勉強し始めた。

数学 表現論

『表現論入門セミナー―具体例から最先端にむかって』の第1章を読み終わりました。

表現論入門セミナー―具体例から最先端にむかって

表現論入門セミナー―具体例から最先端にむかって

Amazon

第1章のまとめ記事をこれまでに2つ書きました。 *1

§1.6を中心に、原子・分子と表現論の関係が書かれています。

物理学と表現論の関係を勉強することがこの本を読むきっかけだったので、本の序盤でこの話が出てきたのはうれしかったです。

その内容について、まとめてみました。

  1. 水素原子
  2. メタン分子
  3. 水素分子（等核2原子分子）
  4. 一酸化炭素分子（異核2原子分子）

第2章からは本格的に表現論の話が始まります。これからが楽しみです！

*1:まだまとめきれていない内容もあります。そのうちに。

球面上の三角形を見ていて思ったこと

数学

子どもたちと直角三角形の話をしていて、球面上に3つの直角を持つ三角形を書くことができることを説明しました。

三角形が書かれたボールをぼんやり眺めていると、いろんなことが頭に浮かんできました。



f:id:wed7931:20181227130508j:plain

幾何学の問題を考えるってこういうことなのかなぁ…と。

頭の中にあることをメモに書いてみました。あまりまとまりがないのはご容赦を。

幾何学への苦手意識が薄れると、こういう発想もできるようで楽しくなってきました。

2018年の数学活動を振り返る。

数学

あと20日ほどで2018年が終わります。

何もしていなかったようで、たぶんいろいろやっていた2018年。

振り返りたいことはたくさんありますが、この1年でやってきた数学の活動について振り返ってみます。


【目次】

MATH POWER 2018に参加

私にとって初めて数学イベントに参加したことが、最も大きな出来事です。

学生時代以来、たっぷりと数学に浸れて、とても幸せな気分でした。

wed7931.hatenablog.com

来年も数学イベントに参加して、今度はいろいろな方と交流できればと思います。

『数学ガール』シリーズのレビューを担当

念願だった『数学ガール』シリーズのレビューを担当することができました。

wed7931.hatenablog.com

非常に貴重な体験でした！

著者の結城浩さんより献本いただいた本は宝物です。

幾何系に興味を持ち始めた

中学以来、幾何学には相当な苦手意識がありました。（こちらに詳しく）

しかし、昨年4月から定期購読している『数学セミナー』の特集や『数学ガール／ポアンカレ予想』を読んで、幾何学に興味が出てきました。

wed7931.hatenablog.com

リーマン計量、ホモトピー、ホモロジーなど、学部時代に理解できなかった内容がようやくわかってきて、幾何学が楽しくなってきました。

wed7931.hatenablog.com

来年もこの流れは続くように思います。

13年ぶりに表現論を勉強し始める

Twitterで数学関係のツイートを見ていると、リー群の表現論と物理との関係が目に付くようになりました。

大学院時代の専門がリー群の表現論だったので、「改めて理解したい！」と思うようになりました。

ということで、私の指導教官が書いた『表現論入門セミナー―具体例から最先端にむかって』を使って、表現論と物理の関係の勉強を10月から始めました。

wed7931.hatenablog.com

ゆっくりと読んでいて、ようやく第1章が読み終わりそうです。
物理との関係も少し出てきて、今後が楽しみです。

数学の本をたくさん買った

ブックオフやメルカリで数学書がかなり安く売っていることを知り、数学の本をたくさん買いました。

学生時代に読んだ教科書や読み物までいろいろ。
今年買った数学関係の本を並べてみると、予想以上にたくさんありました。

ご想像のとおり、ほとんどが積読です。
こういう本は手元にあるだけで落ち着きますね。

さて、2019年は？

2018年は学生時代以降で最もたくさん数学をしました。
興味の範囲も広がり、そのときの興味に応じて、いろいろなことを勉強しました。


そして、2019年。

今と同じように、その時点の興味に応じて勉強して、ブログやTwitterにアウトプットする予定です。

それに加えて、Twitterやイベントなどを通じて、いろいろな方と交流を深めたいです。

頭の中に断片的な知識が散らばった状態になりそうですが、長い時間をかけて知識をつなげて、より広い数学を知ることができればと思います！

それでは、ちょっと早いですが、みなさんよいお年を！

特集「幾何の概念のアイデア」～『数学セミナー2018年12月号』読書メモ その2

数学 数学セミナー 読書メモ

『数学セミナー 2018年12月号』の特集は「幾何の概念のアイデア」です。

数学セミナー 2018年 12 月号 [雑誌]

数学セミナー 2018年 12 月号 [雑誌]

前回のまとめ記事はこちらです。

wed7931.hatenablog.com

今回は、6個の記事のうち中盤の2個のメモを紹介します。

ファイバー束

キーワード

ファイバー束の概念
  • 空間の族や、各点ごとに値域が変わるような一般化された関数を記述するための1つの手法
ファイバー束
  • いわば、「ねじれた直積」を記述する手法
  • ファイバーと局所自明化
ファイバー束の例
  • (1) アニュラス
    • 直積空間であり、大域的な自明化が成り立つ積束の例でもある。
  • (2) メビウスの帯
  • (3) ホップ束
    • 複素射影直線 \mathbb{C}P^1 = \mathbb{C} \cup \{ \infty \} と2次元球面 S^2 の同一視
    • 1点コンパクト化 *1
  • (4) 主 U(1) -束
    • ホップ束の一般化
ファイバー束の構造群
  • 複数のファイバー束の関連を考えるための概念
  • 変換関数
  • 例：ベクトル束、接束、主束
ファイバー束の切断
  • 各点ごとに取る値の空間が変わるような一般化された関数を記述する手法
  • 例：滑らかな多様体上の連続ベクトル場
ファイバー束の分類問題
  • 引き戻し、分類空間、分類写像

イメージしやすいアニュラスとメビウスの帯

今回の連載で、初めてファイバーという概念を知りました。

本文にはアニュラスやメビウスの帯を平行や垂直に切った図が書かれていて、ファイバーの定義と照らし合わせて考えると、非常にわかりやすいのが特徴でした。

私としては、ホップ束や構造群を図としてイメージするのは難しかったですが、数式で追いかけるのはそれほど難しくありませんでした。

接空間をすべて集めた集合の意味合いがわかった

多様体を勉強していくと、滑らかな多様体 M の各点 p \in M における接空間 T_p(M) をすべて集めた集合 TM = \bigcup_{p \in M} T_p M というものが出てきます。

これまで、 TM という集合がどのような場面で使われるかがわからず、なかなか理解しがたいものでした。

ファイバーという概念を「各点ごとに値域が変わるような一般化された関数を記述するための手法」と認識することで、理解を進めることができました。

コホモロジー

キーワード

特異単体とチェイン
  • 標準 k 単体 \Delta^k
    • \Delta^k = \{ (x_i, \dots, x_k) \in \mathbb{R}^{k+1} \ | \ 0 \le x_i , \ \sum_{i=0}^{k} x_i = 1 \}
  • 特異 k 単体
  • （特異） k チェイン
    • 特異 k 単体の \mathbb{R} -係数の形式的な線形結合
    • 特異 k チェイン全体の集合を C_k(M) と書く。
特異コチェインの性質
  • （特異） k コチェイン
    • C_k(M) から \mathbb{R} への線形写像
    • k コチェイン全体の集合を C^k(M) と書く。
  • C_k(M) は C^k(M) の双対空間と言える。
  • M の n-k 次元部分多様体 N を使って M の k コチェイン N^{*} を作る方法
    • 特異 k 単体の像と有限個の点で交わる N の交点の符号を足しあげる。
ポアンカレ双対
  • k コチェイン N^{*} は微分形式で特徴づけられ、これを N のポアンカレ双対という。
    • 本文では、 M と N を特別な場合で説明しているが、一般の多様体でも定義される。
ド・ラームコホモロジー群と特異ホモロジー群

1年前の特集でもホモロジーがあった

『数学セミナー 2017年12月号』の特集で、ホモロジーが扱われていました。

図形的イメージは、2017年12月号でより詳しく書かれています。

そのときのまとめはこちらです。

wed7931.hatenablog.com
wed7931.hatenablog.com

ド・ラームコホモロジーとド・ラームの定理について、今回の記事では数式を使って詳しく書かれています。

*1:松坂和夫『集合・位相入門』 第5章 定理17

*2:いつか、このブログできちんと書いておきたい。

特集「幾何の概念のアイデア」～『数学セミナー2018年12月号』読書メモ その1

数学 読書メモ 数学セミナー

『数学セミナー 2018年12月号』の特集は「幾何の概念のアイデア」です。

数学セミナー 2018年 12 月号 [雑誌]

数学セミナー 2018年 12 月号 [雑誌]

今年は『数学ガール／ポアンカレ予想』などを通して、これまででいちばん幾何学に触れた年だと思っています。

wed7931.hatenablog.com

そこで得られた知識の復習をすることができました。

ここでは、6個の記事のうち2個のメモを紹介します。

曲率の素朴な考え方

キーワード

  • 曲面とその接平面の「違い」から導かれるガウス曲率
  • 測地線：曲面上の2点を結ぶ最短の曲線
  • 曲面上の三角形と平面上の三角形の辺の長さの比較
  • 驚異の定理

『数学ガール／ポアンカレ予想』でも扱われている

ガウス曲率と驚異の定理は『数学ガール／ポアンカレ予想』第8章でも扱われています。

wed7931.hatenablog.com

驚異の定理からわかること

ガウス曲率が曲面上での曲線の長さの情報 *1 から得られるというのが驚異の定理の主張です。

つまり、微分や接平面をうまく定義できないような対象でも曲率を考えることができることがわかります。

微分形式／局所的にも大域的にも便利な道具

キーワード

  • \mathbb{R}^n 上の k 次微分形式（ k -form）
    • wedge積 \wedge が持つ交代性と強い冪零性
  • k 次微分形式全体の集合 A^k(\mathbb{R}^n) は C^{\infty}(\mathbb{R}^n) 加群となる。
  • 直和 \bigoplus_{k=0}^{\infty} A^k(\mathbb{R}^n) は代数をなし、外積代数（グラスマン代数）と呼ぶ。
  • 外微分 d: A^k(\mathbb{R}^n) \to A^{k+1}(\mathbb{R}^n) は dd=0 を満たす。
  • 一般の多様体上の微分形式
    • cotangent bandleのsectionが、局所座標系を使った d x^{i} たちになる。
  • 微分形式の引き戻し（pullback）と押し出し（pushout）
  • 微分形式の積分を定義する手法としての1の分解
  • 微分方程式の弱解とカレント

微分形式と微分方程式の解に関係がある…？

この記事の最後では、微分形式と微分方程式の解の関係が、シュワルツ超関数やカレントという言葉を使って示されています。

いまさらながら、「私の修士論文に大いに関係するのでは？」と思うようになりました。修論を理解したい気持ちがさらに強まりました。

wed7931.hatenablog.com

*1:第一基本形式。『数学ガール／ポアンカレ予想』では、内在的な量と表現しています。